0 views
1. 개요 및 정의
- 한 줄 요약
- 비트는 전구의 스위치(ON/OFF)와 같고, 바이트는 그 스위치 8개를 묶어 문자를 표현하거나 데이터를 저장하는 기본 상자이다.
- 공식 정의:
- 비트(Bit):
- Binary Digit의 약어로, 정보 이론 및 컴퓨팅에서 정보의 가장 작은 단위이다.
- IEC 80000-13 표준에 따라 0 또는 1의 상태를 가진다.
- 바이트(Byte):
- 디지털 정보를 저장하는 데이터의 기본 단위로, 역사적으로는 한 문자를 인코딩하는 데 필요한 비트 수였으나, 현대 컴퓨팅 표준(ISO/IEC 2382)에서는 통상 8비트(Octet)를 1바이트로 정의한다.
- 비트(Bit):
2. 동작 원리
2.1 물리적 계층과 논리적 표현
- 컴퓨터 내부의 CPU와 메모리는 반도체 소자로 구성되어 있다. 논리적인 0과 1은 물리적인 전기 신호로 구현된다.
- 전기 신호:
- 일반적으로 트랜지스터에 일정 전압(예: 5V 또는 3.3V)이 흐르면 1 (High), 흐르지 않으면 0 (Low)으로 인식함.
- 최소 단위:
- 이 하나의 스위치 상태가 1 비트(Bit)이다.
- 주소 지정 단위:
- CPU가 메모리에 접근할 때 비트 단위로 접근하는 것은 비효율적이다.
- 따라서 8개의 비트를 묶어 고유 주소를 부여하고 데이터를 관리하는데, 이것이 1 바이트(Byte)이다.
데이터 표현 범위
- 1 Bit: 21=2가지 (0, 1)
- 1 Byte (8 Bits): 28=256가지 (0 ~ 255)
2.2 진법 변환과 16진수(Hexadecimal)
- 사람은 10진수에 익숙하지만, 컴퓨터는 2진수를 사용한다.
- 2진수는 자릿수가 너무 길어지기 때문에 가독성을 위해 16진수를 널리 사용한다.
- 니블(Nibble):
- 16진수 한 자리는 4비트(반 바이트)에 해당한다. (24=16)
- 변환 매커니즘:
- 1 바이트(8비트)는 16진수 두 자리로 완벽하게 1:1 매핑된다.
[예시: 10진수 60의 변환]
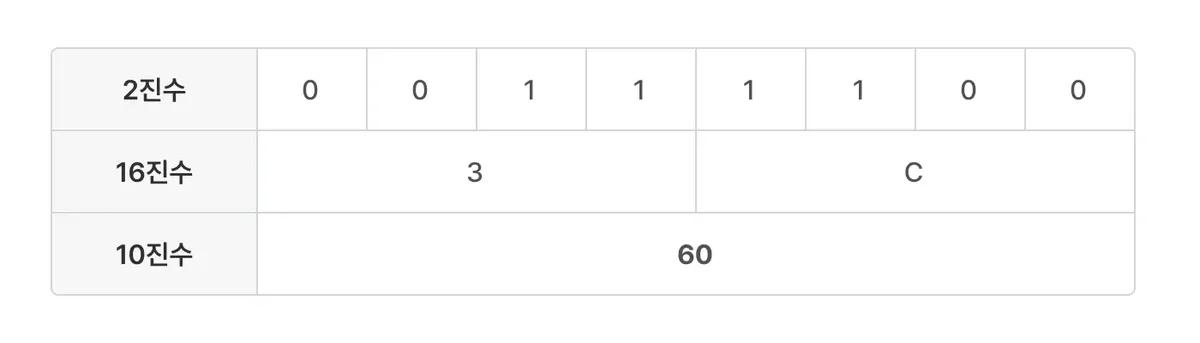
- 10진수: 60
- 2진수:
0011 1100(8비트)- 상위 니블:
0011(21+20=3) → 16진수3 - 하위 니블:
1100(23+22=12) → 16진수C
- 상위 니블:
- 16진수:
0x3C
2.3 비트의 가중치: MSB와 LSB
- 비트의 위치에 따라 데이터 값에 미치는 영향력(Weight)이 다르다. 이를 구분하기 위해 MSB와 LSB를 사용한다.
| 용어 | 전체 이름 | 설명 | 위치 | 영향력 |
|---|---|---|---|---|
| MSB | Most Significant Bit | 최상위 비트 | 가장 왼쪽 (27 자리) | 가장 큼 |
| LSB | Least Significant Bit | 최하위 비트 | 가장 오른쪽 (20 자리) | 가장 작음 |
- MSB의 역할:
- 수의 크기를 결정하는 가장 큰 요소이며, 부호 있는 정수에서는 부호를 결정하는 역할을 겸한다.
- LSB의 역할:
- 값이 홀수인지 짝수인지 판별하는 데 사용할 수 있다. (LSB가 1이면 홀수, 0이면 짝수이다.)
2.4 부호의 표현 (Signed vs Unsigned)
컴퓨터는 음수를 표현하기 위해 MSB를 활용하며, 주로 2의 보수(Two's Complement) 방식을 사용한다.
- Unsigned (부호 없음)
- 모든 비트를 숫자의 크기(Magnitude)로 사용한다.
- 범위 (1바이트 기준): 0 ~ 255 (0 ~ 28−1)
- 예:
10010100= 128+16+4=148
- Signed (부호 있음)
- MSB:
- 0이면 양수, 1이면 음수이다.
- 음수 표현 방식 (2의 보수):
- 비트를 반전시킨 후 1을 더한다.
- 이는 덧셈 연산만으로 뺄셈을 처리하기 위한 하드웨어적 최적화이다.
- 범위 (1바이트 기준): −128 ~ +127 (−27 ~ 27−1)
- 예:
10010100(MSB가 1이므로 음수)- 부호 비트 제외 값 해석이 아님. 2의 보수 역산 필요.
10010100의 2의 보수 →01101011+1=01101100(108)- 결과: −108
- MSB:
3. 사용법 및 구문 (Syntax)
3.1 C/C++에서의 비트 조작 및 타입 선언
- C언어는 메모리 비트 조작에 가장 최적화된 언어이다.
- 아래는 부호 있는 변수와 없는 변수의 차이, 그리고 비트 연산자를 보여준다.
#include <stdio.h>
int main() {
// 1. 부호 있는 타입 (Signed) vs 부호 없는 타입 (Unsigned)
// 2진수 1001 0100 (0x94)
unsigned char u_val = 0x94;
signed char s_val = 0x94;
printf("Unsigned Value: %d\n", u_val); // 출력: 148 (단순 크기)
printf("Signed Value: %d\n", s_val); // 출력: -108 (MSB가 1이므로 음수 처리)
// 2. 비트 마스킹 (Bit Masking) - 특정 비트 확인
// 0x94 = 1001 0100
// LSB 확인 (홀수/짝수 판별)
if (u_val & 0x01) {
printf("LSB is 1 (Odd)\n");
} else {
printf("LSB is 0 (Even)\n"); // 실행됨
}
// MSB 확인 (음수 여부 판별 로직과 유사)
// 0x80 = 1000 0000
if (u_val & 0x80) {
printf("MSB is 1\n"); // 실행됨
}
return 0;
}
3.2 Python에서의 비트 표현
- Python은 기본적으로 정수 오버플로우가 없으나,
bin(),hex()함수를 통해 비트 패턴을 확인할 수 있다.
num = 60
print(bin(num)) # 0b111100 (앞의 00 생략됨)
print(hex(num)) # 0x3c
# 비트 시프트 연산
# 왼쪽으로 1비트 이동 = 값 * 2
print(num << 1) # 120
'Etc'카테고리의 다른 글
Loading comments...